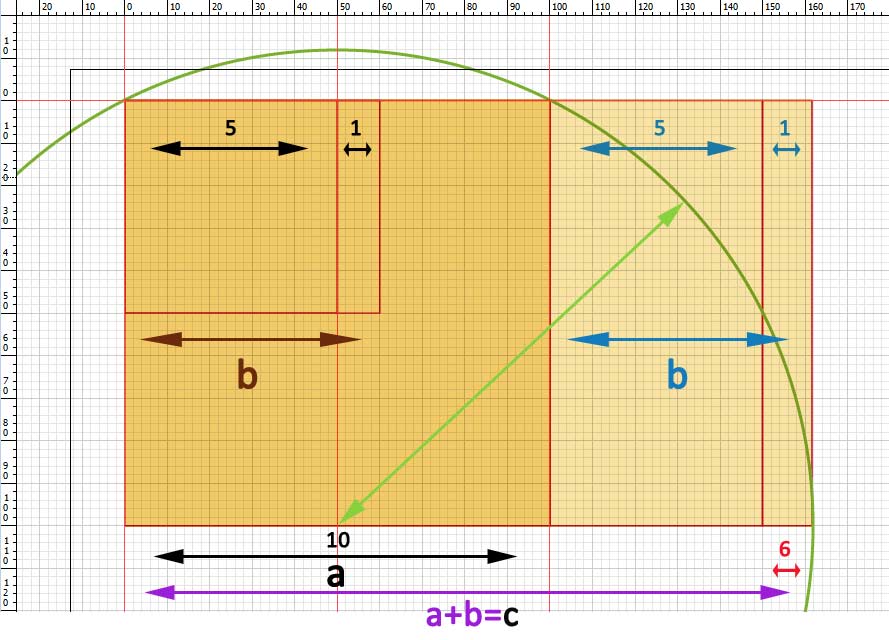
The golden ratio is based on a measure or number also called golden, and represented by the Greek letter φ (fi) (lowercase) o Φ (fi) (capitalize). It is a ratio of roughly: 2 + 1,6 . This means that une mesure a=2 plus another mesure b=1,618…. will be together a mesure of c= 3,618…. Although this is the way that I have invented to quickly understand this ratio and to detect, in a composition, that the golden ratio exists between the measures a, b y c in a image. And, therefore, they have the magical balance where a measurement contains the other plus a little.
The golden ratio mesures:
They say that the golden ratio is an irrational number, which does not fit the exact measurements. And indeed, because the measure b is like a small infinity, because it never ends, and it becames more smaller.
Golden ratio conjugate:
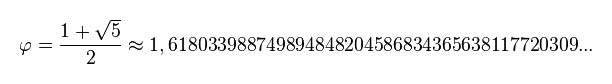
Visual patterns with rectangular golden ratio:
How do you draw the golden ratio?
Easy step by step to draw this “divine proportion” that appears in many natural forms:
- We draw a square with a measure a.
- From the lower base and center of this square, we create a circle that must have the radius just until the corners of the square we are.
- The new circle is bigger that the mesure of a. It give us the point of the new mesure b, by continuing the bottom line of the square just to the point. We have the fragment a + b.
- The vertical rectangle is drawn next to our square.The union of both is the first golden rectangle.
- Inside the rectangle, and from the upper right corner can create a square, whose mesures are the sectionb. And from this second square we start again all the steps , because now we can find the golden section of the new square.
The spiral we build is called golden or Fibonacci Spiral.
Drawing system drawing of a rectangular golden ratio. SVG, scalable vector format.
Visual patterns with triangular golden ratio:
Also called the Aristotle triangle or logarithmic, contains the two measures of a and b.
To create the triangle we use the two measures a and b. Inside, we can draw the Fibonacci spiral like in the square we did.
Golden ratio within a triangle. SVG, scalable vector format.
Other geometric shapes:
The decagon containing 10 golden triangles. SVG, scalable vector format.
As I’m not a mathematician and I get really bad, if someone wants to provide information about the golden ratio it´s ok, because I still have my share difficulties to see quickly their proportions.
This theme continues in Golden spirals on flowers and plants
More information on applications including: http://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html
And on the Wikipedia.